For many students who enter the pit of machine learning, mathematics may be the harder part. The author of this article introduced the mathematical background required to build machine learning products or conduct machine learning research, as well as valuable experience and advice from machine learning engineers, researchers, and teachers, and provided many courses and book resources.
At present, we are not fully aware of the level of mathematics required to start learning machine learning, especially for those who have not studied mathematics or statistics in school.
The goal of this article is to propose the mathematical background needed to build a machine learning product or conduct an academic research on machine learning. These suggestions come from conversations with machine learning engineers, researchers, and educators, as well as the author’s experience in machine learning research and industry.
In order to build the prerequisites for the required level of mathematics, this article first proposes different thinking modes and strategies so that readers can get in touch with mathematics education outside the traditional classroom. Then, the article outlines the specific background required for different types of machine learning projects, as these disciplines range from high school level statistics and calculus knowledge to the latest developments in probabilistic graphical models (PGM). At the end of this, I hope that readers will have a feeling for mathematics learning, and you need to use this knowledge effectively in your machine learning projects, no matter what the project!

First of all, I admit that the personal needs and goals of learners may be unique for learning styles/framework/resources. Welcome everyone to put forward your own opinions on HN!
Some experience about mathematics anxiety
It turns out that many people, including engineers, are afraid of mathematics. First of all, I want to talk about the topic of "good at math".
In fact, people who are good at mathematics will have a lot of practical experience in practical use of mathematics. As a result, they will feel that getting stuck in mathematics is something they take for granted. Recent studies have shown that the learner's mentality (not the innate ability) is the main predictor of a person's ability to learn mathematics.
To be clear, it takes time and energy to achieve this habitually good state, but this is certainly not a natural ability for people. The rest of this article will help readers determine the level of mathematical foundation required and outline strategies for how to establish this level.
Getting started: math and code
As a soft prerequisite, we need readers to master some basic knowledge of linear algebra/matrix operations (so as not to be confused in symbolic representation), and have a preliminary understanding of probability theory. In addition, we encourage you to master basic programming skills as a tool for learning mathematics in a given context. After that, you can adjust your focus according to the type of project you are interested in.
How to learn math outside of school
I believe that the best way to learn math is to study wholeheartedly (ie as a student). If you break away from this full-day learning environment, you may not be able to master the teaching structure in the academic classroom and gain (positive) pressure from your peers and available resources.
If you want to study mathematics outside of school, I suggest organizing study groups, luncheons, and study seminars as an important resource to gain motivation for learning. In research laboratories, reading groups can also be organized. In terms of learning structure, your reading group can browse the chapters of the textbook, hold regular discussion lectures, and open up channels to hold Q&A questions and answers.
Here, culture plays an important role. This kind of "extra" learning should be encouraged, so as not to forget what you have learned in the day-to-day complicated affairs. In fact, despite the short-term costs of this approach, building a peer-driven learning environment can make your long-term work more efficient.
Math and code
Mathematics and code are highly integrated in the machine learning workflow. Code is usually constructed directly using mathematical intuition, and the code even shares some symbols and syntax with mathematics. In fact, modern data science frameworks (such as NumPy) make the readable code converted into mathematical operations (such as matrix/vector products) more intuitive and efficient.
The author encourages readers to use code as a way to consolidate learning. Both mathematics and code depend on the accuracy of understanding and representation. For example, the manual implementation of the practical loss function or optimization algorithm can be a good way to truly understand the basic concepts.
Here let us give a specific example of learning mathematics through code: back propagation of ReLU activation in a neural network (yes, it can be done through Tensorflow/PyTorch! For details, see the link https://medium.com/@karpathy /yes-you-should-understand-backprop-e2f06eab496b). Backpropagation is a technique that relies on the calculus chain rules to efficiently calculate gradients. In order to use the chain rule under this setting, we multiply the upstream derivative with the gradient of ReLU.
First, we visualize the activation of ReLU, as shown in the figure:
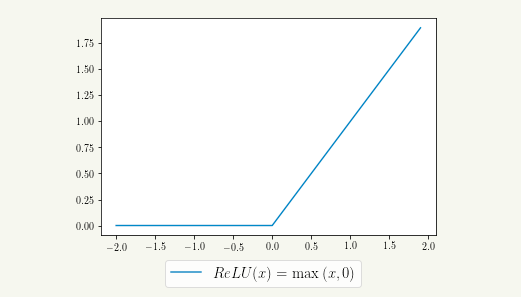
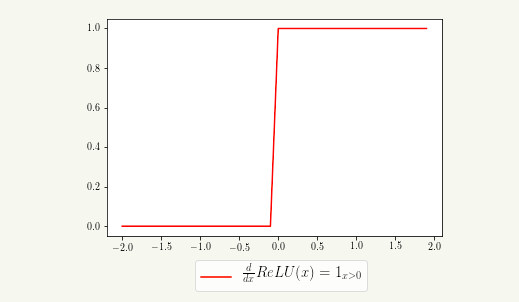
In order to calculate the gradient (intuitively, the slope), a piecewise function can be visualized, expressed as an index function as follows:
NumPy provides us with a useful and intuitive syntax. Our activation function (blue curve) can be explained in the code, where x is the input and relu is the output:
relu=np.maximum(x,0)
Then there is the gradient (the red curve in the figure), where grad represents the upstream gradient:
grad[x
Without first deriving the gradient yourself, the meaning of this line of code may not be so obvious. In our code, for all elements that meet the conditions, all values ​​in the upstream gradient (grad) are set to 0, [h
As seen above, through our basic understanding of calculus, we can clearly think about the code. The completed example of neural network implementation is here: https://pytorch.org/tutorials/beginner/pytorch_with_examples.html
Mathematical knowledge required to build machine learning products
When writing this section, I consulted a machine learning engineer to determine how to best use mathematics to debug the system. The following question example is a reply given by an engineer from a mathematical perspective. It doesn't matter if you have never seen it before, I hope this chapter can provide some appropriate background for the specific issues you are interested in.
Which clustering method should I use to display high-dimensional customer data?
Method: PCA and tSNE
How should I calibrate the threshold for "stopping" fraudulent user transactions?
Method: Probability Calibration
How to correctly describe the deviation of satellite data in different regions of the world? (Such as Silicon Valley and Alaska)
Method: Make the research question public. For example, the equalization of demographic informatics?
Generally, statistical tools and linear algebra can be applied to each of these problems in some way. However, to get a satisfactory answer, you usually need to target a specific method in a specific field. In this case, how should you determine what mathematics you need to learn?
Define the system
The resources we can use now are very rich (for example, scikit-learn for data analysis, keras for deep learning), which helps readers start writing code to model the system. When using these resources, you can try to answer the following related questions:
1. What is the input/output of the system?
2. How should the data be prepared to adapt to the system?
3. How to construct functions or plan data to help the model to generalize?
4. How to define reasonable goals for the questions asked?
You may be surprised, it may be difficult to define the system! After that, the engineering required for pipeline construction is also very important. In other words, building machine learning products requires a lot of heavy work, which does not require an in-depth mathematical background.
More information: •BestPracticesforMLEngineeringbyMartinZinkevich,ResearchScientistatGoogle
Learn math on demand
The first thing to look at is the workflow of machine learning. You may find that you get stuck in some steps, especially when debugging. When you are trapped, do you know what to look for? How reasonable is your weight? Why can't your model be integrated with a specific loss definition? What is the correct way to measure the success of the model? At this time, it may be helpful to make assumptions about the data, constrain optimization in different ways, or try different algorithms.
Usually, you will find mathematical intuitions (such as how to choose loss functions and evaluation metrics) in the modeling/debugging process, and these intuitions may help make smart engineering decisions. These are your opportunities to learn!
Rachel Thomas from Fast.ai is a supporter of this "learning on demand" approach. When educating students, she found that it is more important for deep learning students to get excited about these materials. After the interest is established, mathematics education becomes an on-demand search for vacancies.
more info:
Course: ComputationalLinearAlgebrabyfast.ai
YouTube:3blue1brown:EssenceofLinearAlgebraandCalculus
Textbook: LinearAlgebraDoneRightbyAxler
Textbook: ElementsofStatisticalLearningbyTibshiranietal.
Course: Stanford'sCS229 (MachineLearning) CourseNotes
Mathematical knowledge required for machine learning research
The author now wants to describe which mathematical thinking styles are useful for research-oriented work in machine learning. The pessimistic view on machine learning research is reflected in plug-and-play systems, in which the model will invest more computing power to squeeze higher performance. In some populations, researchers are still skeptical of empirical methods that lack mathematical rigor (such as certain deep learning methods).
The future research system may be based on existing systems and assumptions, and these systems and assumptions will not expand our basic understanding of the field, which is worrying. Researchers need to provide original resources and build new infrastructure modules that can be used to gain new perspectives and methods to achieve practical goals. For example, it may be necessary to rethink the building blocks of convolutional neural networks for image classification, as the "father of machine learning" Geoff Hinton said in his recent paper on CapsuleNetworks. (Link to the paper: https://arxiv.org/pdf/1710.09829v1.pdf)
Next, we need to ask basic questions. This requires "deep understanding" in mathematics, and Michael Nielsen, the author of "Deep Learning", calls it "interesting exploration". This process involves often being “stuck with difficult problems†for thousands of hours, constantly asking questions, and changing perspectives when exploring new problems. "Interesting exploration" enables scientists to ask deep, insightful questions, not just a simple idea/architecture combination.
Of course, it is obvious that you still can't learn everything when studying machine learning! To do "interesting exploration" correctly, you need to do it appropriately, you need to follow your own interests, rather than prioritize the hottest new results.
Machine learning research is a very rich research field, and there are pressing problems in fairness, interpretability, and accessibility. In fact, in all scientific disciplines, basic thinking is not an on-demand process, but patience is required to use the breadth of the advanced mathematics framework to think and solve critical problems.
More information: • Blog: DoSWEsneedmathematics? by KeithDevlin • Reddit post: ConfessionsofanAIResearcher • Blog: HowtoReadMathematics by ShaiSimonson and FernandoGouvea • Paper: NIPSandICML and other conference papers
• Article: AMathematician'sLamentbyPaulLockhart1
Democratize machine learning research
I hope I did not describe "research mathematics" too esoteric, because the views constructed using mathematics should be presented in an intuitive form! Unfortunately, many machine learning papers are still full of complex and inconsistent terminology, making key information difficult to distinguish. As a student, you can use blogs, tweets, etc. to translate condensed papers into easy-to-digest and understand points of view, which is also doing good for yourself and the field. You can even use distill.pub as an example, which is a publication dedicated to providing clear explanations of machine learning research results. In other words, if the mystery of technical thought can be turned into a means of "interesting exploration", it will be very helpful!
Some final conclusions and suggestions
In short, I hope this article can provide readers with a starting point for readers to consider mathematics education issues related to machine learning.
Different problems require different degrees of intuitive views, and I encourage readers to first figure out what the goal is.
If you want to build a machine learning product, please find peers and study groups through questions, and stimulate your learning through in-depth research on the ultimate goal.
In the field of research, having a deep mathematical foundation can provide you with a wealth of tools to promote the development of machine learning by proposing new infrastructure modules.
Generally speaking, mathematics (especially mathematics in research papers) can be daunting, but getting stuck in learning is an important part of the learning process.
FTTx Accessories Clamps & Hooks
Galvanized Steel Pole Clamp,Steel Drop Wire Clamp,Galvanized Steel Hoop Fastening Retractor
Sijee Optical Communication Technology Co.,Ltd , https://www.sijee-optical.com