OpenAI researchers have recently released a highly optimized GPU computing kernel that supports a neural network architecture that has barely been explored: networks with sparse block weights. Depending on the degree of sparsity, these cores can run an order of magnitude faster than cuBLAS or cuSPARSE. OpenAI researchers have used these cores to achieve top results in text sentiment analysis and text image generation.

In the field of deep learning, the development of model architectures and algorithms is largely governed by the extent to which the GPU supports basic computing operations. Specifically, one of the problems is that the computational efficiency is too low when implementing sparse linear operations through the GPU. OpenAI's release of the computing kernel is to support this, but also contains some initial results of a variety of sparse modes. These results have shown some potential, but they are not decisive evidence. OpenAI researchers are also inviting more researchers in the field of deep learning to join hands and continue to improve the computing core to make more computing architectures possible.
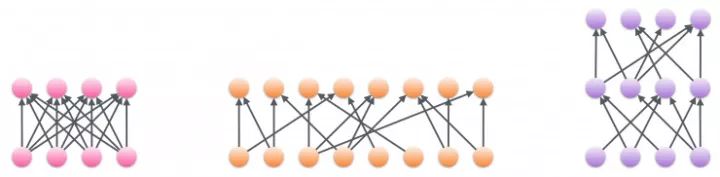
A densely connected layer (left side) can be replaced with a sparse, wider layer (middle) or a sparse, deeper layer (right side), while the calculation time is almost constant
The sparse weight matrix is ​​significantly different from the dense weight matrix, where many of the values ​​are zero. The sparse weight matrix is ​​the basic component that many models aspire to, because the computational cost of matrix multiplication and convolution operations involving sparse blocks is only proportional to the number of non-zero numbers in the block. An obvious benefit of sparsity is the ability to train neural networks that are much wider and deeper than others, given the number of parameters and computational resource constraints, such as implementing LSTM with tens of thousands of hidden layer neurons. Network (the current training LSTM has only a thousand hidden neurons).
Computing kernel

Schematic diagram of a dense weight matrix (left) and a sparse block weight matrix (middle). The white area means that the corresponding position in the weight matrix is ​​0.
This compute kernel allows the full join and convolution layers to efficiently utilize sparse block weights. For convolutional layers, the input and output feature dimensions of this kernel can be sparse; connectivity in the spatial dimension is not affected. The definition of sparsity is defined at the level of the block (above right), and is optimized for blocks of size 8x8, 16x16, 32x32 (8x8 blocks are shown here). At the block level, sparse mode is completely configurable. Since this kernel directly skips blocks with a value of 0 during computation, the computational resources consumed are only proportional to the number of non-zero weights, rather than proportional to the number of output/output features as before. The overhead of storing these parameters is also proportional to the number of non-zero weights.
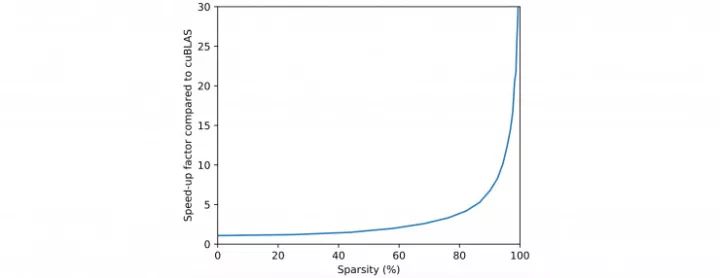
The acceleration factor of this kernel at different sparse ratios compared to cuBLAS. Test conditions: Wide neural network (12288 hidden layer neurons), block size 32x32, mini-batch size 32; test hardware for NVIDIA Titan X Pascal GPU, CUDA version 8.0. At these sparse ratios tested, the speed increase ratio is higher than cuSPARSE.
Apply this computing kernelOpenAI researchers have also shown some sample code for sparse matrix multiplication in TensorFlow.
Import tensorflow as tf
Import numpy as np
Hidden_size = 4096
Block_size = 32
Minibatch_size = 64
# Create a (random) sparsity pattern
Sparsity = np.random.randint(2, size=(hidden_size//block_size,hidden_size//block_size))
# Initialize the sparse matrix multiplication object
Bsmm = BlocksparseMatMul(sparsity, block_size=block_size)
# Input to graph
x = tf.placeholder(tf.float32, shape=[None, hidden_size])
# Initialize block-sparse weights
w = tf.get_variable("w", bsmm.w_shape, dtype=tf.float32)
# Block-sparse matrix multiplication
y = bsmm(x, w)
# Run
Sess = tf.InteractiveSession()
Sess.run(tf.global_variables_initializer())
Result = sess.run([y], feed_dict = {x: np.ones((minibatch_size,hidden_size), dtype='float32')})
Print(result)
Miniature LSTM
A very interesting use of the sparse block kernel is to create a miniature neural network. The thumbnails can be connected together, and any two nodes in the diagram can be connected in a few steps, even if the entire graph has billions of nodes. The reason that OpenAI researchers want to achieve such a miniature connection is that even if the network is highly sparse, they still want information to spread quickly throughout the picture. The human brain has shown a miniature connection mode, which also brings about the question of whether the performance of LSTM can be improved if it has the same characteristics. Through the application of miniature sparse connectivity, OpenAI researchers efficiently trained LSTM models with approximately 20,000 hidden layer neurons, while the width of the network was also five times wider than the network with a similar total number of parameters. The trained network has better performance in text generation modeling and semi-supervised emotion classification.

In the thumbnail, even if the sparseness is high, only a small number of steps between nodes can be connected to each other. The above image shows the activation of the central node (pixel) from the two-dimensional Watts-Strogatz thumbnail; and a random smoothing for a better look. In this picture, the average path length between different nodes is less than 5, similar to the Barabasi-Albert diagram in OpenAI researchers' LSTM experiments.
Emotional representation learningOpenAI researchers trained sparse block weight networks and dense weight matrix networks with similar parameters to compare their performance. The sparse model performs better on all emotional data sets. On the IMDB dataset, this sparse model of OpenAI dramatically reduced the previous best 5.91% error rate to 5.01%. Compared with OpenAI, some experiments have only performed well in short sentences, and this time also shows potential results in long sentences.
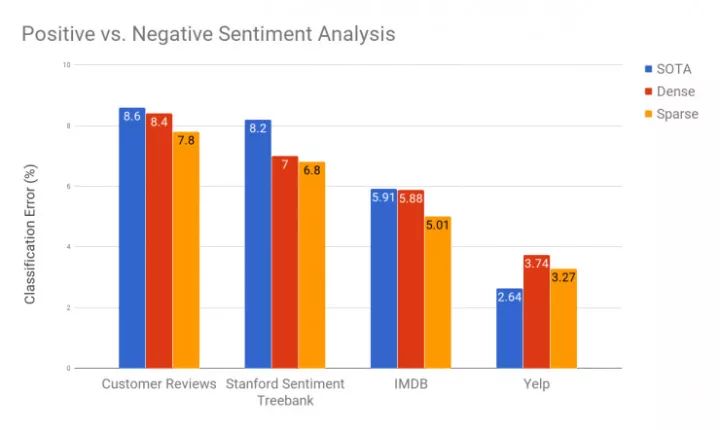
Emotional classification results of linear models of feature training based on generative dense and sparse model extraction. The dense and sparse models here have almost equal number of parameters.
Compression task performanceWith the sparse, wider LSTM model, the compression of the number of bits per character was improved from 1.059 to 1.048 in the experiment, again on a model with a similar number of parameters. This result can be further improved if the linear layer structure with sparse blocks is replaced by a densely connected linear layer. OpenAI researchers made a simple modification to the PixelCNN++ model for CIFAR-10, replacing the normal 2D convolution kernel with a sparse kernel while keeping the network deeper while keeping other hyperparameters unchanged. . The modified network also reduced the number of bits per dimension from 2.92 to 2.90, achieving the best results on this data set.
Future research directionMost of the weights in the neural network can be pruned after the training is over. If the pruning action is used in conjunction with this sparse kernel, how much computation time can be saved and how much calculation speed can be improved?
In the biological brain, part of the sparse structure of the network is determined at the time of growth (another role of growth is to change the strength of the connection). Is there a similar approach in artificial neural networks, that is, not only through gradient learning to connect weights, but also to learn the optimal sparse structure? A recent paper has proposed a method for learning sparse block RNN. OpenAI has recently proposed an algorithm for L0 normalization in neural networks, both of which can play a role in this direction.
OpenAI researchers have trained LSTM models with tens of thousands of hidden layer neurons to bring better text modeling performance. More broadly, models with large weight matrices can maintain the same number of parameters and computational overhead as smaller models if sparse layers are used. I believe there must be some areas that can make this approach a big part.
Stainless Steel Industrial Pipe
ShenZhen Haofa Metal Precision Parts Technology Co., Ltd. , https://www.haofametal.com