About Fourier transform transform?
Answer: The fourier transform transforms the continuous time domain signal into the frequency domain; it can be said to be a special case of the laplace transform. The laplace transform is a generalization of the fourier transform. The existence condition is wider than that of the fourier transform. It transforms the continuous time domain signal to Complex frequency domain (the entire complex plane, and the fourier transform can be regarded as only on the jΩ axis at this time); z transform is the laplace transform of the discrete signal after ideal sampling of the continuous signal, and then the transform result when z=e^sT (T is the sampling period), the corresponding domain is the digital complex frequency domain, at this time the digital frequency ω=ΩT. ——Reference Zheng Junli's "Signal and System".

2. What is Laplace Transformation? answer:

(1) The solving equation is simplified. And the initial conditions are automatically included in the transformation formula.
(2) Laplace transform transforms "differential" into "multiplication" and "integral" into "division". That is, the differential equation becomes an algebraic equation. The Laplace transform transforms the convolution operation in the time domain into a "multiplication" operation.
(3) Analyze the laws of the system by using the zero and pole distribution of the system function.
In the classic control theory, the analysis and synthesis of the control system are all based on the Laplace transform. One of the main advantages of introducing the Laplace transform is that transfer functions can be used instead of differential equations to describe the characteristics of the system. This is to use an intuitive and simple graphical method to determine the entire characteristics of the control system (see signal flow chart, dynamic structure diagram), analyze the movement process of the control system (see Nyquist stability criterion, root locus method), and The correction device of the integrated control system (see the control system correction method) provides the possibility.
Now give you an example: when we are learning control, for example, the differential equation of a second-order circuit RLC system is: LC*Uc''+RC*Uc'+Uc=U If you take this differential equation harder, then you use Laplace transformation, the differential equation becomes LC*s^2*Uc+RCs*Uc+Uc=U and then Uc=U/(LCs^2+RCs+1) and then you can look up the table to get the result directly (just look up the integral table Just as convenient), isn’t this much better than solving differential equations for you!
(Second statement) Laplace transform provides a method of transforming the domain of definition, mapping the signal (function) defined in the time domain to the complex frequency domain (to understand this sentence, you need to understand the function space The concept of-we know that a function defines a relationship "from an element of a set to an element of another set", and a set composed of two or more functions is a function space, that is, a function space is also a set ; The "domain" of the Laplace transform is the function space. It can be said that the Laplace transform is a function of processing functions. Since the Laplace transform is well defined, it has some peculiarities Characteristics), and this is a one-to-one correspondence (as long as the convergence region of the complex frequency domain is given), so as long as a time-domain function (signal) is given, it can be transformed to one by Laplace transform Complex frequency domain signal (regardless of whether the signal is a real signal or a complex signal), therefore, as long as we process the complex frequency domain signal, it is equivalent to processing the time domain signal (for example, let f(t)â†â†’F( s), Re[s]>a, then if we delay F(s) to get the signal F(sz), Re[s]>a+Re[z], then it is equivalent to giving the time domain The function is multiplied by a rotation factor e^zt, that is, f(t)e^ztâ†â†’F(sz), Re[s]>a+Re[z]; as long as F(sz) is inversely transformed, you can get f(t)e^zt).
Laplace transform is used to solve differential equations, mainly by applying several properties of Laplace transform, turning solving differential equations into solving algebraic equations (because solving algebraic equations is always much easier than solving differential equations! Moreover, (It can be very convenient) to perform the inverse Laplace transform on the solution result to obtain the solution of the original differential equation).
We can always easily draw a picture of a real variable function (most functions do), but it is difficult for us to draw a picture of a complex variable function. This may be one of the reasons why the Laplace transform is more abstract; Another reason is that the complex frequency s in the Laplace transform has no clear physical meaning. Regarding characteristic roots and complex numbers, it is recommended that the questioner read the definitions in the book. It should not be difficult to understand. 3. What is z-transform?

4. What is FFT (Fast Fourier Transform)? Answer: Commonly used in audio processing. It is to transform the waveform (time domain signal) to the frequency domain, so that users can analyze it better. The frequency domain is similar to the frequency spectrum of "Tianqian Listening". This process is called "Discrete Fourier Transform" (DFT). And FFT is an efficient and fast algorithm of DFT. The principle of the Fast Fourier Transform algorithm is (from Baidu Encyclopedia): Fast Fourier Transform (FFT) is a fast algorithm for discrete Fourier transform, which is based on the odd, even, imaginary, real and other characteristics of discrete Fourier transform. The transformation algorithm is improved. It has no new discoveries about the theory of Fourier transform, but it can be said to be a big step forward for applying discrete Fourier transform in computer systems or digital systems. Let x(n) be a complex number sequence of N terms, transformed by DFT, any calculation of X(m) requires N complex number multiplications and N-1 complex number additions, and one complex number multiplication is equal to four real number multiplications and two Real number addition,
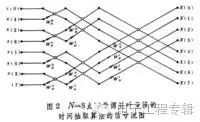

One complex number addition is equal to two real number additions. Even if one complex number multiplication and one complex number addition are defined as one "operation" (four real number multiplications and four real number additions), then find the X(m) of the N-term complex number sequence, that is N-point DFT transformation requires approximately N2 operations. When N=1024 points or more, N2=1048576 operations are required. In FFT, using the periodicity and symmetry of WN, a sequence of N items (set N=2k, k is a positive integer) is divided into Two sub-sequences of N/2 items, each N/2-point DFT transform requires (N/2) 2 operations, and then N operations are used to combine the two N/2-point DFT transforms into one N-point DFT Transform. After this transformation, the total number of operations becomes N+2(N/2)2=N+N2/2. Continuing the above example, when N=1024, the total number of calculations becomes 525312, saving about 50% of the calculation. And if we continue to carry on the idea of ​​"dividing one into two" until it is divided into two groups of DFT operation units, then the DFT transformation of N points only needs Nlog2N operations, and when N is at 1024 points, the operation The amount is only 10240 times, which is 1% of the previous direct algorithm. The more points, the greater the savings in calculations. This is the superiority of FFT.
2.54mm Pitch
2.54mm Pitch
ATKCONN ELECTRONICS CO., LTD , https://www.atkconn.com