Hamiltonian graph: A loop of graph G, if it passes through each node of the graph once, and only once, is the Hamiltonian loop. The graph in which the Hamiltonian loop exists is the Hamiltonian graph. The Hamiltonian chart starts from a point, passes all the necessary and only once, and finally returns to the starting point. Some edges in the picture may not pass, but no edges will be passed twice.
The difference with the Euler diagram: The Euler diagram is actually about the feasible convenience of the edge on the graph, and the requirements of the Hamilton diagram are related to the point.
One: Dirac theorem (sufficient conditions)
Two: basic necessary conditions
Let G = "V, E" be a Hamiltonian graph, then for any non-empty subset S of v, if |S| represents the number of elements in S, GS means that the points in S are deleted in G and these points The subgraph obtained after the associated edge is W(GS) "=|S| is established. Where W(GS) is the number of Unicom branches in the GS.
Three: competition map (Hamilton pathway)
There is a Hamiltonian path at the N(N)=2) order map.
Algorithm: One: Constructing a Hamiltonian loop under the premise of Dirac's theoremprocess:
1: Arbitrarily find two adjacent nodes S and T, and extend a path that is as long as possible without duplicate nodes. That is, if S is adjacent to node v, and v is not on path S - "T, then the path can be changed to v - "S -" T, then v becomes a new S. S and T are respectively extended to both ends Until the expansion cannot continue, that is, all nodes adjacent to S or T are on the path S - "T.
2: If S is adjacent to T, the path S - "T" forms a loop.
3: If S and T are not adjacent, a loop can be constructed. Let path S - "T have k + 2 nodes, followed by S, v1, v2, . . . , vk, T. can prove that the existence node vi (i belongs to [1, k]), satisfies vi adjacent to T, and vi+1 is adjacent to S. Find this node vi and change the original path to S - " vi - " T - " vi+1 - " S , which forms a loop.
4: So far, a loop with no repeating nodes has been constructed. If the length is N, the Hamilton loop is found. If the length of the loop is less than N, since the entire map is connected, there must be a point on the loop adjacent to the point outside the loop. Then, when the loop is disconnected from this point, it changes back to a path, and the adjacent point can also be added to the path. Then follow the steps in step 1 to extend the path as much as possible, and new nodes must be added. Then go back to path 2.
prove:
Can be proved by the pigeon nest principle.
Fake code:
Let s be the starting point of the Hamiltonian loop, and t be the point before the end point s in the Hamiltonian loop. Ans[] is the final Hamiltonian loop. Inverted means the order in which the numbers in the interval corresponding to the array are arranged.
1: Initialize, let s = 1, t be any adjacent point of s.
2: If the number of elements in ans[] is less than n, then expand outward from t. If there is an expandable point v, put the tail of ans[], and t=v, and continue to expand, if it cannot expand. Step 3.
3: Invert the currently obtained ans[], s and t are interchanged, and expand outward from t. If there is an expandable point v, put the end of ans[], and t=v, and continue to expand. If you cannot expand to step 4.
4: If the current s and t are adjacent, go to step 5. Otherwise, traverse ans[], find the point ans[i], so that ans[i] is connected to t and ans[i +1] is connected to s, from ans [i + 1] to the ans[] in the t part, t=ans[i +1], proceed as in step 5.
5: If the number of elements in the current ans[] is equal to n, the algorithm ends, and the Hamilton circuit is saved in ans[] (see whether the situation is added to the point s). Otherwise, if s is connected to t, but the number of elements in ans[] is less than n, then traversing ans[], looking for the point ans[i], causing ans[i] to be connected to a point (j) outside of ans[] , then let s=ans[i - 1], t = j, ins[s] ans[] in ans[] to ans[i - 1], inans[] to a part of t in ans[] Invert, add point j to the end of ans[], go to step 2.
time complexity:
If every time you go to step 5 to calculate a round, then since at least one node in each round is added to the path S - "T, the total number of rounds must not exceed n rounds, so the time complexity is O ( n^2). Since the number of edges is very large in space, it is more suitable to use the adjacency matrix for storage.
Code:
Const int maxN = 100;
Inline void reverse(int arv[maxN + 7], int s, int t){// reverse the order of the array anv from subscript s to t
Int temp;
While(s " t ) {
Temp = arv[s];
Arv[s] = arv[t];
Arv[t] = temp;
s++;
T--;
}
}
Void Hamilton(int ans[maxN + 7], bool map[maxN + 7][maxN + 7], int n){
Int s = 1, t; / / initialize the s to point 1
Int ansi = 2;
Int i, j;
Int w;
Int temp;
Bool visit[maxN + 7] = {false};
For(i = 1; i <<= n; i++) if(map[s][i]) break;
t = i; / / take any adjacency and s point is t
Visit[s] = visit[t] = true;
Ans[0] = s;
Ans[1] = t;
While(true){
While(true){//extends from t
For(i = 1; i <<= n; i++){
If(map[t][i] && !visit[i]){
Ans[ansi++] = i;
Visit[i] = true;
t = i;
Break;
}
}
If(i 》 n) break;
}
w = ansi - 1; / / invert the currently obtained sequence, s and t are interchangeable, continue to expand from t, equivalent to scale out from s on the original sequence
i = 0;
Reverse(ans, i, w);
Temp = s;
s = t;
t = temp;
While(true){// continues to scale out from the new t, which is equivalent to scaling out from s on the original sequence
For(i = 1; i <<= n; i++){
If(map[t][i] && !visit[i]){
Ans[ansi++] = i;
Visit[i] = true;
t = i;
Break;
}
}
If(i 》 n) break;
}
If(!map[s][t]){//If s and t are not adjacent, adjust
For(i = 1; i " ansi - 2; i++)// takes a point i in the sequence such that ans[i] is connected to t and ans[i+1] is connected to s
If(map[ans[i]][t] && map[s][ans[i + 1]])break;
w = ansi - 1;
i++;
t = ans[i];
Reverse(ans, i, w);//Invert from ans[i +1] to ans[]
}//At this time s and t are connected
If(ansi == n) return;//If the current sequence contains n elements, the algorithm ends
For(j = 1; j <<= n; j++){//The number of elements in the current sequence is less than n, finding the point ans[i], causing ans[i] to be connected to a point other than ans[]
If(visit[j]) continue;
For(i = 1; i " ansi - 2; i++)if(map[ans[i]][j])break;
If(map[ans[i]][j]) break;
}
s = ans[i - 1];
t = j; / / assign the newly found point j to t
Reverse(ans, 0, i - 1);//Invert the part of s to ans[i-1] in ans[]
Reverse(ans, i, ansi - 1);//Invert the part of ans[i] to t in ans[]
Ans[ansi++] = j;//Add point j to the end of ans[]
Visit[j] = true;
}
}
Two: N (N = 2) step competition map construction Hamiltonian pathN-order competition map : a directed graph with N vertices with an edge between each pair of vertices. There must be a Hamiltonian path for the N-order race map.
The mathematical induction method proves that the competition map must have Hamiltonian road when n ′ = 2:
(1) When n = 2, the conclusion is clearly established;
(2) Assuming that n = k, the conclusion is also true, and the Hamilton road is V1, V2, V3, . . . , Vk;
Let n + k+1, the k + 1th node is V(k+1), considering the connection between V(k+1) and Vi(1"=i"=k), it can be divided into the following Two situations.
1: The arc between Vk and V(k+1) is "Vk, V(k+1)", then the Hamiltonian paths V1, V2, ..., Vk, V(k+1) can be constructed.
2: The arc between Vk and V(k+1) is "V(k+1), Vk", then look for the first Vi that appears from the back (i=k-1,i"= 1,--i), satisfying the arc between Vi and V(k+1) is "Vi,V(k+1)", then constructing the Hamiltonian path V1, V2, ..., Vi, V(k+1 ), V(i+1), ..., V(k). If Vi is found that satisfies the condition, it means that for all Vi (1 "=i"=k) to V(k+1) arcs are "V(k+1), V(i)", then construct Hami The path V(k+1), V1, V2, ..., Vk .
The algorithm for constructing the Hamiltonian road in the competition map is the same as the above proof process.
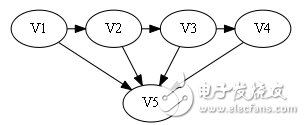
Use the diagram to illustrate:
Assume that there is already a path V1 - " V2 - " V3 - " V4 at this time. There are 16 kinds of connection between these four points and V5. Given four numbers consisting of 0/1, the ith number is 0. Arc "V5, Vi", and vice versa 1, indicating the presence of arc "Vi, V5"
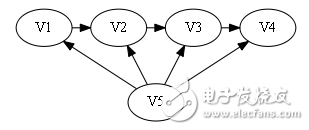
Sign[]={0, 0, 0, 0}.
Obviously, it belongs to the second case. It can't find 1 from the back, that is, there is no arc "Vi, V5".
Then construct the Hamilton Road: V5 - "V1 -" V2 - "V3 -" V4.
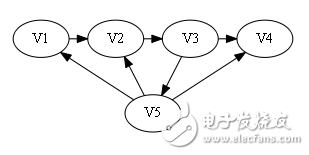
Sign[]={0, 0, 0, 1}.
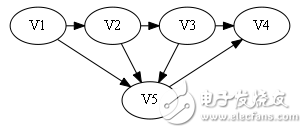
In the first case, the last number is 1, which means that there is an arc "Vi, V5" and i = 4 (last point)
Then construct the Hamilton Road: V1 -》 V2 -》 V3 -》 V4 -》 V5.
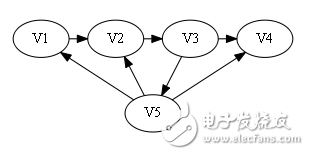
Sign[]={0, 0, 1, 0}.
In the second case, the first position that appears 1 from the back is 3.
Construct Hamilton Road: V1 -》 V2 -》 V3 -》 V5 -》 V4.
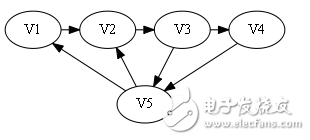
Sign[]={0, 0, 1, 1}.
In the first case, the last number is 1, which means that there is an arc "Vi, V5" and i = 4 (last point)
Then construct the Hamilton Road: V1 -》 V2 -》 V3 -》 V4 -》 V5.
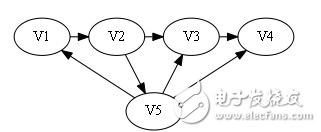
Sign[]={0, 1, 0, 0}.
In the second case, the first position that appears 1 from the back to the front is 2.
Construct Hamilton Road: V1 -》 V2 -》 V5 -》 V3-》 V4.
Sign[]={0, 1, 0, 1}.
In the first case, the last number is 1, which means that there is an arc "Vi, V5" and i = 4 (last point)
Then construct the Hamilton Road: V1 - "V2 -" V3 - "V4 -" V5. (I will not mention the chestnut at the end of the ~~)

Sign[]={1, 0, 1, 0}.
In the second case, the first position that appears 1 from the back is 3.
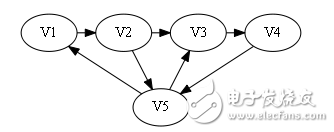
Construct Hamilton Road: V1 -》 V2 -》 V3 -》 V5-》 V4.
Sign[]={1, 1, 1, 0}.
In the second case, the first position that appears 1 from the back is 3.
Construct Hamilton Road: V1 -》 V2 -》 V3 -》 V5-》 V4.
Sign[]={1, 1, 1, 1}.
The same last bit is 1, which means "Vi, V5" and i=4 (last)
Then construct the Hamiltonian road: V1 - "V2 -" V3 - "V4 -" V5. The above is the process of describing the algorithm when N=4 (N+1=5).
Note that looking forward from the back is not the point before the number of this point, that is, not by number, but by the current Hamiltonian sequence from the back. Give a chestnut:
4
twenty one
1 3
3 2
4 1
4 2
4 3
First step ans={1}
The second step iss={2,1}
The third step sign={0, 1}(map[3][2] = 0,map[3][1] = 1, the current sequence is 2,1) instead of {1, 0}(1,2 ), because there are arcs "V1, V3" and "V3, V2". Need to pay attention here.
Code:
#include 《iostream》
#include 《cmath》
#include 《cstdio》
#include 《cstring》
#include 《cstdlib》
#include "algorithm"
#include "queue"
#include "stack"
#include "vector"
Using namespace std;
Typedef long long LL;
Const int maxN = 200;
//The arv[] length is len, insert key befor arv[index]
Inline void Insert(int arv[], int &len, int index, int key){
If(index 》 len) index = len;
Len++;
For(int i = len - 1; i 》= 0; --i){
If(i != index && i)arv[i] = arv[i - 1];
Else{arv[i] = key; return;}
}
}
Void Hamilton(int ans[maxN + 7], int map[maxN + 7][maxN + 7], int n){
Int ansi = 1;
Ans[ansi++] = 1;
For(int i = 2; i <<= n; i++){//The first case, directly add the current point to the end of the sequence
If(map[i][ans[ansi - 1]] == 1)
Ans[ansi++] = i;
Else{
Int flag = 0;
For(int j = ansi - 2; j 》 0; --j){// In the current sequence, the first point j that satisfies the condition is found from the back to the front, so that "Vj, Vi" and "Vi," exist. Vj+1".
If(map[i][ans[j]] == 1){// After finding it, insert the point before the j + 1 point of the sequence.
Flag = 1;
Insert(ans, ansi, j + 1, i);
Break;
}
}
If(!flag)Insert(ans, ansi, 1, i);//Otherwise, all points are adjacent to point i, and the point is inserted directly into the beginning of the sequence.
}
}
}
Int main()
{
//freopen("input.txt", "r", stdin);
Int t;
Scanf("%d", &t);
While(t--){
Int N;
Scanf("%d", &N);
Int M = N * (N - 1) / 2;
Int map[maxN + 7][maxN + 7] = {0};
For(int i = 0; i " M; i++){
Int u, v;
Scanf("%d%d", &u, &v);
//map[i][j] is 1 for j "i, and there is an arc "Vi, Vj" because only the position of all points before the point is considered when inserting, and it has nothing to do with the subsequent points. So only focus on the connection between this point and its previous point.
If(u " v)map[v][u] = 1;
}
Int ans[maxN + 7] = {0};
Hamilton(ans, map, N);
For(int i = 1; i <<= N; i++)
Printf(i == 1 ? "%d": "%d", ans[i]);
Printf("");
}
Return 0;
}
Code 2: void Hamilton(int ans[maxN + 7], int map[maxN + 7][maxN + 7], int n){
Int nxt[maxN + 7];
Memset(nxt, -1, sizeof(nxt));
Int head = 1;
For(int i = 2; i <<= n; i++){
If(map[i][head]){
Nxt[i] = head;
Head = i;
}else{
Int pre = head, pos = nxt[head];
While(pos != -1 && !map[i][pos]){
Pre = pos;
Pos = nxt[pre];
}
Nxt[pre] = i;
Nxt[i] = pos;
}
}
Int cnt = 0;
For(int i = head; i != -1; i = nxt[i])
Ans[++cnt] = i;
}
Code three:
Void Hamitton(bool reach[N + 7][N + 7], int n)
{
Vector "int" ans;
Ans.push_back(1);
For(int i=2;i <<= n;i++)
{
Bool cont = false;
For(int j=0;j"(int)ans.size()-1;j++)
If(reach[ ans[j] ][i] && reach[i][ ans[j+1] ])
{
Ans.insert(ans.begin()+j+1,i);
Cont = true;
Break;
}
If(cont)
Continue;
If(reach[ ans.back() ][i])
Ans.push_back(i);
Else
Ans.insert(ans.begin(),i);
}
For(int i=0;i"n;i++)
Printf("%d%c",ans[i],i==n-1?'':' ');
}
Single-Element Detector,Hortwave Detector Unit,Swir Infrared Detector,Swir Ingaas Unit Detector
Ningbo NaXin Perception Intelligent Technology CO., Ltd. , https://www.nicswir.com