Recently, I have a colleague who always asks me "Why do we use so many activation functions?", "Why is this function better than that?", "How do you know which function to use?", "Is this difficult math?" "and many more. So I think, why don't I write an article about people who have a basic understanding of neural networks, and introduce the activation function and the corresponding mathematics?
Note: This article assumes that you have a basic understanding of artificial "neurons."
Activation function
Simply put, artificial neurons calculate the "weighted sum" of the input, plus the offset, and then decide whether you need to "activate" (well, the activation function actually determines whether to activate, but let us understand this now).
Consider a neuron.
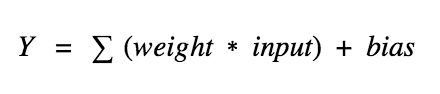
In the above formula, the value of Y may be any value between negative infinity and positive infinity. Neurons do not know the boundaries of values. So how do we decide if a neuron needs activation?
To this end, we decided to add an "activation function".
Step function
The first thing we think of is a threshold-based activation function. If the value of Y is greater than a specific value, it is defined as "active". If it is less than the threshold, it is not activated.
Activation function A = "active" if Y > threshold else not
Or, A = 1 if Y > threshold, otherwise 0
Ok, we just defined a step function.
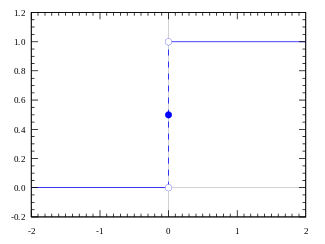
When the value is greater than 0 (threshold), the output is 1 (active), otherwise the output is 0 (inactive).
well. It is clear that this can be used as an activation function for neurons. However, this method has some specific drawbacks.
Suppose you are creating a binary classifier that outputs "yes" or "no" (activated or not activated). A step function can do this. In fact, this is exactly what the step function does, outputting 1 or 0. Then, think about if you want to connect more of these neurons to introduce more categories, such as class 1, class 2, class 3, and so on. What happens when more than one neuron is "activated"? All neurons will output 1 (based on the step function). Then how do you decide which classification the final result belongs to? Well, it's hard, it's complicated.
You may want to use the if and only when one neuron output is 1 to indicate the classification result. what! This is harder to train. A better option is that the activation function is not binary and can express concepts such as "50% activation" and "20% activation". In this way, when more than one neuron is activated, you can find the "most active" neuron (in fact, the better choice than max is softmax, but we will use max now).
Of course, if more than one neuron indicates "100% activation", the problem still exists. However, because there is an intermediate value in the output, the learning process will be smoother and easier (less fluctuating), and the probability of 100% activation of more than one neuron is much less than that of using step function training (of course, it depends on training) The data).
Ok, so we want to output the intermediate (analog) activation value instead of just outputting "active" or "inactive" (binary value).
The first thing we thought of was a linear function.
Linear function
A = cx
The above is a straight line function, and the activation is proportional to the function input (the weighted sum of the neurons).
So this will give a range of activations instead of binary activation. We can of course connect several neurons, and if more than one neuron is activated, we can make a decision based on the maximum (max or softmax). So this is good. So, what is the problem with this?
If you are familiar with the gradient descent used for training, you will notice that the derivative of this function is a constant.
The derivative of A = cx versus x is c. This means that the gradient is independent of x. This will be a constant gradient. If the prediction is wrong, the changes made by backpropagation will be constant, independent of the input delta(x)! ! !
This is not so good! (Not always, but please allow me to say that.) In addition, there is still a problem. Think about the layers that are connected. Each layer is activated by a linear function. This activation is then used as the input to the next layer, and the next layer is also activated based on the linear function, repeating the process until the last layer.
No matter how many layers we have, if the activation functions of these layers are linear, the final activation function of the last layer will be the linear function of the input of the first layer! Pause for a while, think about this.
This means that the two layers (or N layers) can be replaced by a single layer. what! We have just lost the ability to stack network layers. Regardless of how many layers we stack, the entire network is always equivalent to a single-layer neural network with linear activation (the linear combination of linear functions is still a linear function).
Let's go ahead.
Sigmoid function
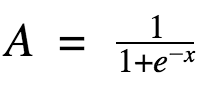
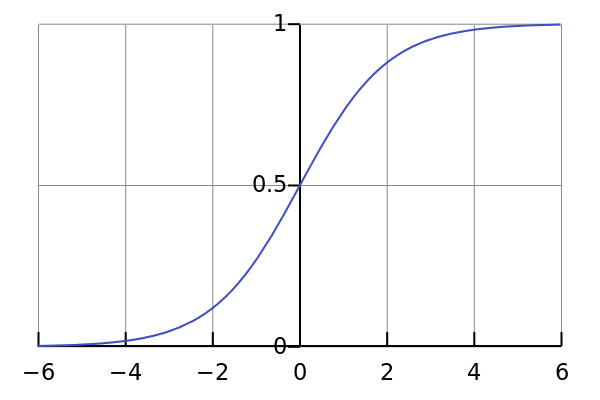
Ok, this curve looks smooth, a bit like a step function. So what are the benefits? Take a moment to think about it.
First of all, it is non-linear. This means that the combination of functions is also non-linear. awesome! We can stack the network layer. As for nonlinear activation? Yes, it is nonlinear activation! Unlike the step function, it gives the analog activation. At the same time, it also has a smooth gradient.
I don't know if you noticed it. When X is between -2 and 2, the value of Y is very steep. This means that any small change in X in this interval will cause a significant change in Y. This means that the function tends to direct the value of Y towards both ends of the curve.
It seems that this property is useful for classifiers? That's right! Indeed it is. It tends to activate both sides of the guide curve. This creates a clear difference in the predictions.
Another advantage is that the value range of the function is (0, 1) relative to the range of linear functions (-inf, inf). So our activation function is bounded.
The sigmoid function is one of the most widely used functions now. So, what is the problem with it?
I don't know if you noticed it, the closer it is to the two ends of sigmoid, the more N changes toward X. This means that the gradient in this area will be small. This is the "gradient gradient" problem. Well, so what happens when the activation function is close to the "near horizon" part of the curve?
The gradient will be small or disappear (because the value is so small that no significant changes can be made). The network refuses to learn further, or the learning speed is drastically slow (depending on the specific case, until the gradient/calculation hits the limit of the floating point value). However, we have some workarounds, so sigmoid is still very popular in the classification problem.
Tanh function
Another common activation function is the tanh function.
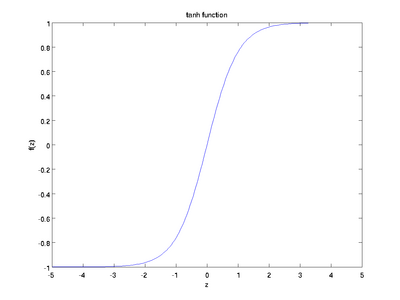
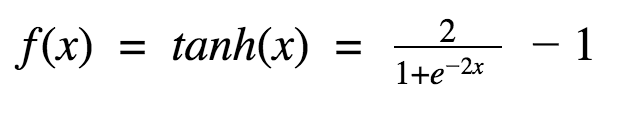
Well, this looks a lot like sigmoid. In fact, this is a sigmoid function that has been pulled up!
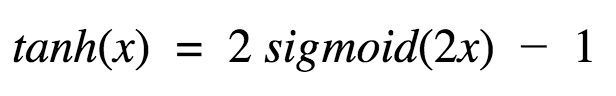
Well, the nature of tanh is similar to the sigmoid we discussed earlier. It is non-linear, so we can stack the network layer. It is bounded (-1, 1), so don't worry about activation expansion. It is worth mentioning that the tanh gradient is more intense than the sigmoid (the derivative is steeper). Therefore, choosing sigmoid or tanh will depend on your need for gradient strength. Similar to sigmoid, tanh also has a gradient attenuation problem.
Tanh is also a very popular and widely used activation function.
ReLu
Next, it is the ReLu function,
A(x) = max(0, x)
The ReLu function is shown above. When x is positive, it outputs x, otherwise it outputs 0.
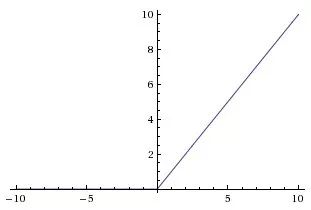
At first glance this has the same problem as a linear function because it is linear at positive values. First, RuLu is nonlinear. The combination of ReLu is also non-linear! (Actually it's a good approximation. The combination of ReLu can approximate any function.) Very good, which means we can stack the network layer. However, it is not bounded. The range of ReLu is [0, inf). This means it will bloat the activation function.
Another point I want to point out is the sparsity of activation. Imagine a large neural network with many neurons. Using sigmoid or tanh causes almost all neurons to be activated in an analog manner (not forgotten?) This means that almost all activations need to be processed to describe the output of the network. In other words, activation is intensive. This is costly. Ideally, we want some neurons in the network to be inactive, making activation sparse and efficient.
ReLu is very useful in this regard. Imagine a network with random initial weights (or normalized weights) based on the characteristics of ReLu (the negative value of x will output 0), and basically 50% of the networks will generate zeros. This means that fewer neurons will be activated (sparse activation) and the network will be lighter. Wow, great! ReLu looks really good! Yes, it's really good, but nothing is flawless... even RuLu.
The horizontal portion of ReLu (negative value of X) means that the gradient will tend to zero. When the horizontal area located in ReLu is activated, the gradient will be zero, causing the weight to not be adjusted with the gradient. This means that neurons trapped in this state will stop responding to errors/inputs (very simple, because the gradient is 0, nothing changes). This is called the death ReLu problem. This problem can cause some neurons to die directly and lose their response, causing a large part of the network to enter a passive state. There are some ReLu variants that alleviate this problem, turning the horizontal line to a non-horizontal part, for example, y = 0.01x when x < 0, changing the image from a horizontal line to a slightly inclined line. This is the weak correction ReLu (leaky ReLu). There are other variations. The main idea is to make the gradient non-zero so that the network can gradually recover from training.
Compared to tanh and sigmoid, ReLu is more economical because it uses relatively simple mathematical operations. This is an important factor to consider when designing deep neural networks.
Ok, which one to choose?
Now consider the question of which activation function to use. Should we always use ReLu? Or sigmoid or tanh? Ok, it is not. When we know that a function that is trying to approximate has certain properties, we can choose an activation function that can approximate the function faster, thus speeding up the training process. For example, sigmoid is very effective for classifiers (look at the sigmoid image, does it show the nature of an ideal classifier?), because sigmoid-based combination approximations are easier to classify functions than functions like ReLu. . Of course, you can also use your own custom functions! If you are not sure about the nature of the function you are trying to learn, then I would suggest starting with ReLu and then try the other. In most cases, ReLu works well as a general approximation.
In this article, I tried to describe some common activation functions. There are other activation functions, but the basic idea is the same. Research to find better activation functions is still ongoing. I hope you understand the idea behind the activation function, why use the activation function, and how to use the activation function.
Pvc Conduit Pipe,Plastic Conduit Pipe,Electrical Wiring Pipe,Plastic Cable Conduit
FOSHAN SHUNDE LANGLI HARDWARE ELECTRICAL CO.LTD , https://www.langliplastic.com