â€Content:
8.1 Optimization Objection
8.2 Large margin intuition
8.3 Mathematics Behind Large Margin Classification
8.4 Kernels
8.5 Using a SVM
8.5.1 Multi-class Classification
8.5.2 Logistic Regression vs. SVMs
8.1 Optimization Objection
Support Vector Machine (SVM) is a very useful supervised machine learning algorithm. First, let's review the logistic regression. According to the log() function and the nature of the Sigmoid function, there are:
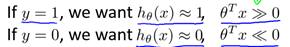
At the same time, the cost function of the logistic regression (not regularized) is as follows:
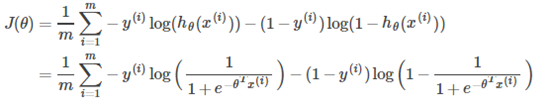
To get the cost function of the SVM, we make the following changes:
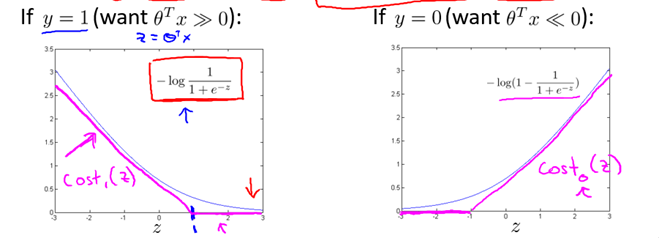
Therefore, compare Logistic's optimization goals
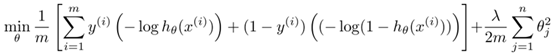
The optimization goals of SVM are as follows:
Note 1: In fact, the Cost0 and Cost1 functions in the above formula are a surrogate loss function called hinge loss. Other common substitution loss functions have exponential loss and rate loss. For details, see Machine Learning. P129 Zhou Zhihua)
Note 2: Pay attention to the correspondence between parameters C and λ: C is positively correlated with (1 / λ).
8.2 Large margin intuition
According to the cost function in 8.1, in order to minimize the cost function, the following conclusions are made:
Now suppose C is large (such as C = 100,000), in order to minimize the cost function, we hope
So the cost function becomes:
So the problem becomes:
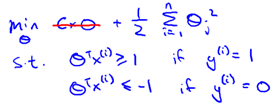
The final optimization result of this problem is to find a partitioned hyperplane with "maximum margin", so the support vector machine is also called the large margin classifier. So what is the interval? Why can I find the maximum interval for this optimization? First, we intuitively feel through the two-dimensional 0/1 linear classification shown in Figure 8-1.
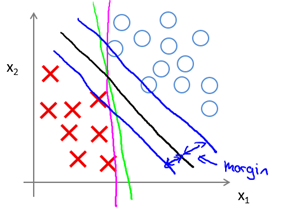
Figure 8-1 SVM Decision Boundary: Linearly separable case
Intuitively, we should look for the dividing hyperplane located in the "positive middle" of the two types of training samples, that is, the black line (two-dimensional) of Figure 8-1, because the "tolerance" of the local plane perturbation of the training sample is best. . For example, the pink and green lines in the graph, once the input data changes slightly, will get a wrong prediction. In other words, the classification result produced by this partitioning hyperplane is the most robust and has the strongest generalization ability to predict the data set. The distance between the two blue lines is called the margin. The next section will explain the optimization principle of interval and maximum interval from a mathematical point of view.
8.3 Mathematics Behind Large Margin Classification
First introduce some mathematics.
2-norm: It can also be called length. It is a generalization of the length of a two-dimensional or three-dimensional space vector. The vector u is denoted by ||u||. For example, for a vector u = [ u1, u2, u3, u4], ||u|| = sqrt(u1^2 + u2^2 + u3^2 + u4^2)
Vector Inner Product: Let vector a = [a1, a2, ..., an], vector b = [b1, b2, ..., bn], and the inner product of a and b is defined as: a · b = A1b1 + a2b2 + ... + anbn . The vector inner product is a generalization of the geometric product scalar product (dot product), which can be understood as the product of the projection length (norm) of the vector a on the vector b and the length of the vector b.
So have:
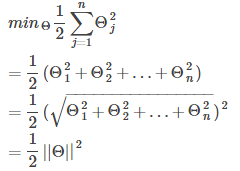
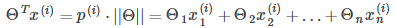
among them 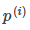 Yes
Yes 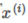 in
in  The length of the projection on the vector.
The length of the projection on the vector.
Therefore, the optimization problem obtained in Section 8.2 can be converted into the following form:
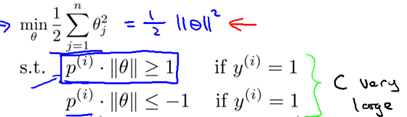
The dividing line is 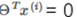 So I know
So I know 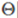 And the boundary line is orthogonal (vertical), and when
And the boundary line is orthogonal (vertical), and when 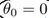 When the boundary line crosses the origin (European space). To optimize the target (take the minimum) and satisfy the constraints,
When the boundary line crosses the origin (European space). To optimize the target (take the minimum) and satisfy the constraints, 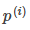 It should be as large as possible, so that the spacing is as large as possible. Intuitive as shown in Figure 8-2, the left side of the figure is a small spacing, at this time
It should be as large as possible, so that the spacing is as large as possible. Intuitive as shown in Figure 8-2, the left side of the figure is a small spacing, at this time 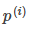 Smaller, in order to satisfy the constraint, the objective function becomes larger, and the right side of the figure is the maximum spacing.
Smaller, in order to satisfy the constraint, the objective function becomes larger, and the right side of the figure is the maximum spacing. 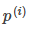 It is the biggest, so the goal can be as small as possible.
It is the biggest, so the goal can be as small as possible.
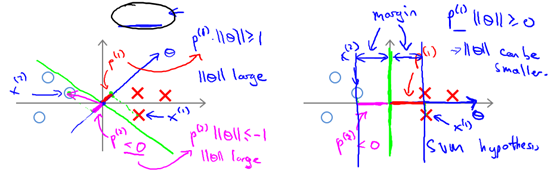
Figure 8-2 Two different spacing situations
8.4 Kernels
The above discussion is based on linearly separable samples, that is, there is a divided hyperplane that can correctly classify training samples. However, there are a lot of complex, nonlinear classification problems in the real world (such as XOR/Same or Problem in Section 4.4.2). ). Logistic regression can deal with nonlinear problems by introducing polynomial feature quantities as new feature quantities; neural networks solve nonlinear classification problems by introducing hidden layers and layer-by-layer evolution; while SVM solves nonlinear problems by introducing kernel functions. . The specific practices are as follows:
For a given output x, specify a certain number of landmarks, recorded as 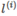 ;
;
Put x, 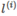 As a kernel function input, get a new feature quantity
As a kernel function input, get a new feature quantity 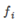 If the kernel function is recorded as similarity(), then
If the kernel function is recorded as similarity(), then
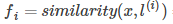 ,among them
,among them 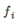 versus
versus 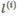 One-to-one correspondence;
One-to-one correspondence;
Substituting the new feature quantity for the original feature quantity, the hypothesis function is as follows:
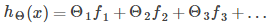
There are two problems now,
How to choose landmarks?
What kind of kernel function is used?
For the first question, you can use the input of the training set as landmarks as follows
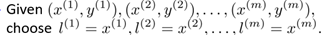
Therefore, the number of feature quantities is equal to the number of training sets, that is, n = m, so the SVM with the kernel becomes the following form:

For the second problem, the commonly used kernel functions are linear kernel, Gaussian kernel, polynomial kernel, Sigmoid kernel, Laplacian kernel, etc., and the commonly used Gaussian kernel is taken as an example.
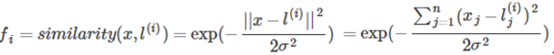
The Gaussian kernel has the following properties:
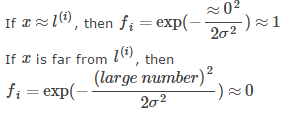
That is, if x and landmark are close, then the value of the kernel function is that the new feature will be close to 1, and if x and landmark are far apart, the value of the kernel function will be close to zero.
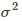 It is a parameter of the Gaussian kernel, and its size will affect the speed of the change of the kernel function. Specifically, Figure 8-3 is a special case of a two-dimensional case, but the properties contained are generalizable. which is
It is a parameter of the Gaussian kernel, and its size will affect the speed of the change of the kernel function. Specifically, Figure 8-3 is a special case of a two-dimensional case, but the properties contained are generalizable. which is 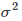 The larger, the slower the change (decrease) of the kernel function, and vice versa.
The larger, the slower the change (decrease) of the kernel function, and vice versa. 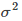 The smaller the kernel function, the faster the kernel function changes.
The smaller the kernel function, the faster the kernel function changes.
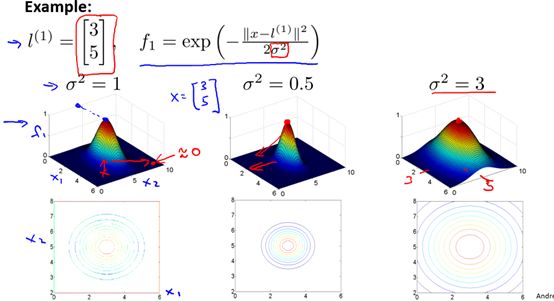
Figure 8-3 Example of the effect of parameters on a Gaussian kernel
How to choose parameters?
The following is a brief analysis of the effects of SVM parameters on deviations and variances:
C: Since C and (1 / λ) are positively correlated, the analysis of λ in combination with Section 6.4.2 is:
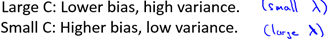

8.5 Using a SVM
The above briefly introduces the optimization principle of SVM and how to use the kernel function. In the actual application of SVM, we do not need to implement the SVM training algorithm to get the parameters.  Usually use existing packages (like liblinear, libsvm).
Usually use existing packages (like liblinear, libsvm).
But the following work is what we need to do:
Select the value of parameter C
Select and implement a kernel function
If the kernel function takes parameters, you need to select the parameters of the kernel function, such as the Gaussian kernel needs to be selected. 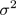
If there is no core (select linear kernel), that is, a linear classifier is given, which is suitable for the case where n is large and m is small.
Select a nonlinear core (such as a Gaussian kernel) for n small and large m
Here are some things to note:
Normalize feature quantities before using kernel functions
Not all functions are valid kernel functions, they must satisfy the Mercer theorem.
If you want to get the parameters of the parameter C or kernel function through training, it should be done on the training set and the cross-check set, see section 6.3.
8.5.1 Multi-class Classification

8.5.2 Logistic Regression vs. SVMs

We are professional audio manufacturing company that makes a variety of speaker with bluetooth, including bluetooth portable speaker, bluetooth speakers outdoor, small speaker bluetooth, light bluetooth speakers, waterproof speakers etc.
With full turnkey service from product design to delivery, and every step in between.
From sophisticated custom audio systems to 'off-the-shelf' speaker drivers, iTopnoo has been saving our customers time, effort, and money.
To constantly offer clients more innovative products and better services is our consistent pursuit.
Best Portable Speakers,customizable bluetooth speaker, Custom jbl speakers, speaker wholesalers
TOPNOTCH INTERNATIONAL GROUP LIMITED , https://www.micbluetooth.com